
어제의 Algorithm 영상에 이어, 오늘은 그 다음 차례인 Data Structure를 공부하고 정리하여 포스팅 하려고 한다.
Crash Course 영상의 특징은 핵심을 잘 짚어 주는 애니메이션이라고 생각하는데, 이것이 글로만 보거나 말로만 들을 때보다 이해를 빠르게 할 수 있도록 도와 준다. 또한 짧지만 압축적으로 많은 정보를 10분 내외로 전달하는데 이 때 애니메이션이 10분 간 집중력을 유지할 수 있도록 큰 도움이 된다.
Data Structures
우리는 데이터가 엉망 진창으로 있는 것이 아니라, 읽고 불러오기 쉽도록 구조가 잘 정리되어 있기를 바란다. 이것을 위해 Data Structure를 이용한다.
Arrays
다른 말로 list 혹은 vector라고도 하는 배열은 메모리에 연속적으로 저장된 값을 말한다.
j=5처럼 한 개의 변수에 한 개의 값을 저장하는 것 대신, 여러 개의 숫자를 지정한 다음 배열 변수(array variable)에 저장할 수 있다.
배열에 있는 특정한 값을 찾으려면 index를 지정해 주어야 한다. 프로그래밍에서 대부분의 배열은 0부터 시작하며 배열의 크기를 [ ] 로 표현한다.
배열은 매우 다양한 방면으로 사용되기 때문에 이것을 유용하게 다룰 수 있는 함수들이 많다. 거의 모든 프로그래밍 언어에는 배열을 입력하면 정렬이 되는 정렬 기능이 내장되어 있다.
String
문자열 역시 배열의 한 종류이다. String은 Null character 즉 0으로 끝나도록 되어 있는데, 이것은 "character로서의 0"이 아닌, "binary로서의 0"이다. 이것은 문자열의 끝을 알려 주기 때문에 중요하다. 예를 들어 print를 쓸 때 이것이 없다면 메모리 안의 모든 문자를 다 출력하게 될 것이다.
String Concatenation (strcat)

문자열 역시 정말 많이 쓰이기 때문에, 문자열만 다루는 함수도 굉장히 많다. 예를 들어 많은 프로그래밍 언어에는 두 문자열을 입력받아 두 번째 문자열을 첫 번째 문자열의 끝에 복사해 주는 String Concatenation, 또는 strcat이라고 하는 함수를 가지고 있다.
Matrix : Array or Array

매트릭스는 스프레드시트의 표나 화면의 픽셀처럼 2차원으로 확장된 자료를 다루고 싶을 때 유용하다. 이것은 배열의 배열이라고 보면 되는데, 3 x 3 matrix는 크기가 3인 배열이 3개 있는 것을 뜻한다.
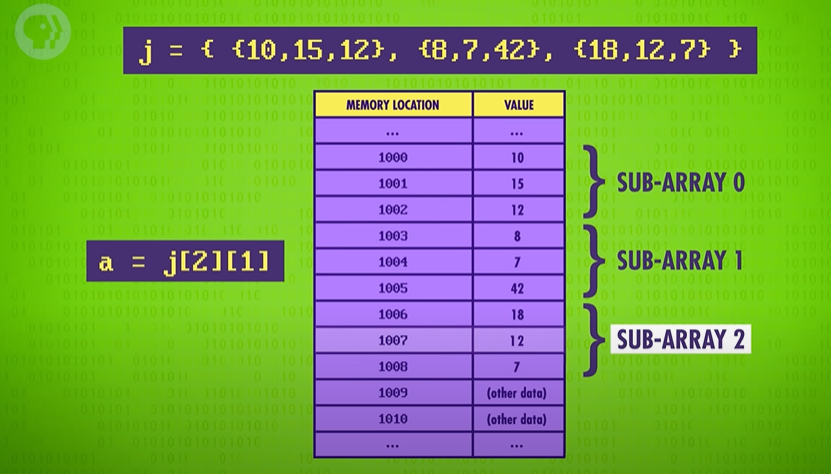
메모리 상에는 값이 이런 식으로 저장되어 있는데, 특정 값에 접근하려면 인덱스 두 개를 알려 주어야 한다. 예를 들어 j[2][1] 을 찾는다면 2번째 배열에서 위치 1의 값을 구하는 것이다. 이렇게 값 12를 찾을 수 있다.
매트릭스의 장점은 배열의 크기를 제한하지 않는다는 것이다. 얼마든지 만들고 싶은 크기나 차원으로 만들어 낼 수 있다. 예를 들어 5차원 배열(five dimensional matrix)를 만들고 싶다면 이렇게 선언해 주면 된다. a = j[2][0][18][13][1]
Struct

연관성 있는 자료를 연결해서 데이터들을 저장할 수 있을까? 이 문제를 해결하기 위해 구조체라는 것이 도입되었다. 은행 계좌번호와 잔액을 함께 저장하는 것이 가능해졌다.
변수의 그룹은 struct로 묶을 수 있다. 이제 여러 데이터들을 한 번에 저장 가능한 복합 데이터로 된 변수를 만들어 낼 수 있다.
구조체 또한 배열로 만들어 자동으로 묶을 수도 있다. 만약 j[0]을 찾으려고 한다면, 전체 구조체가 저장된 곳에서 계좌번호와 잔고, 두 정보를 다 찾아낼 수 있다. 구조체의 배열은 만들어질 때 크기가 고정되고, 더 많은 아이템을 넣기 위해 확장될 수는 없다. 게다가 배열은 메모리에 순서대로 저장되어야 하기 때문에, 중간에 새로운 값을 넣기가 어렵다. 그러나 struct data structure는 이러한 제약 사항을 피하기 위해 더욱 복잡한 data structure를 빌딩하는 데 이용할 수 있다.
Node
이것도 역시 struct의 한 종류인데, variable과 pointer를 저장하고 있다. pointer란 그 지점(point)의 특별한 변수여서 붙여진 이름인데, 메모리의 주소를 가리킨다.
Linked List
struct를 이용해서 linked list(연결 리스트)를 만들 수 있다. 이것은 많은 node들을 저장할 수 있는 유연한 data structure이다. 이것은 각 노드가 목록의 다음 노드를 가리키도록 함으로써 실행된다. 이렇게 linked list는 원형(circular)이 된다. 하지만 다음 포인터 값을 0(null)로 해 줌으로써 linked list를 끝낼 수도 있다. null의 값은 끝에 도달했다는 것을 나타낸다.
프로그래머가 연결 리스트를 사용할 때는, 다음 목록에 저장된 메모리 값을 거의 보지 못한다. 대신 그림처럼 추상화된 연결 리스트를 사용해서 훨씬 쉽게 개념화 할 수 있다.
크기를 미리 지정해 줘야 하는 배열과는 달리, 연결 리스트는 크기를 상황에 따라 늘리거나 줄일 수 있다. 예를 들어, 메모리에 새 노드를 할당하고 연결 리스트에 삽입할 수 있다. 단지 다음 포인터를 변경하는 것만으로 말이다.
연결 리스트는 쉽게 순서를 바꾸거나, 간략화, 쪼개기, 뒤집기 등등이 가능하다. 정렬 알고리즘에도 유용하게 쓰인다. 이러한 유연성 때문에 더욱 복잡한 자료 구조들이 연결 리스트의 위에 구축되었다. 가장 유명하고 보편적인 것은 큐과 스택이다.
Queue : First In First Out (FIFO)
우체국에 사람들이 줄을 서 있는 것처럼, 도착한 순서대로 들어간다. 가장 오래 기다리던 사람이 가장 먼저 서비스를 받는다. 앞에 있는 사람이 얼마나 오래 걸리든간에 그냥 기다려야 한다.
Stack : Last In First Out (LIFO)
작은 변화를 주면 linked list를 LIFO 형식인 Stack처럼 사용할 수 있다.
큐에 더하고 빼는 대신, 스택에서 데이터는 push로 추가되고 pop으로 제거된다.
Trees
- 가장 위에 있는 노드를 root라고 한다.
- 한 노드에서 뻗어져 나오는 노드들은 children nodes라고 한다.
- 이들 위에 있는 노드를 parent nodes라고 한다.
- 맨 끝의 노드는 leaf nodes라고 한다.
한 노드는 두 개 까지의 자식을 가질 수 있을 때, 이 구조체를 binary tree라고 한다. 하지만 상황에 맞게 자료 구조를 수정함으로써 트리의 자식 노드 수를 3이나 4 혹은 임의의 수로 늘릴 수 있다. 심지어 연결 리스트를 써서 그들이 가리키는 모든 노드를 저장하는 트리 노드도 만들 수 있다.
트리 구조에서 중요한 것은 - 현실과 자료 구조에서 - 바로 뿌리에서 잎까지 하나의 길이 존재한다는 것이다. 뿌리가 나뭇잎과 연결되어 있고, 뿌리와 연결되면 이상할 것이다.
무한 루프와 같이 제멋대로 연결되는 자료들은 대신 그래프 데이터 구조를 사용한다. 이것은 root, leaf, parent, children에 대한 개념이 없다. 어떠 것이든 아무거나 포인터로 가리킬 수 있다.
Red-black Trees & Heaps
이것은 위에서 설명한 기본적인 뼈대 위에 프로그래머들이 만든 똑똑한 변형이다.
자료구조마다 특정 계산에 유용한 속성을 가지고 있다. Data Structure를 잘 선택한다면 일을 쉽게 처리할 수 있다. 그래서 실전으로 돌입하기 전, 이론을 배우는 것이 중요하다.
많은 프로그래밍 언어는 라이브러리에 이미 만들어진 자료구조들이 많다.
- C++ : Standard Template Libaray
- Java : Java Class Library
즉 프로그램을 맨 처음부터 만드느라 시간을 낭비하지 않아도 된다는 뜻이다.
자료구조의 힘을 사용해 흥미로운 일들을 할 수 있다. 새로운 추상화의 레벨로 올라가는 것이다. New Level of Abstraction!
Reference :
'Computer Science > Crash Course' 카테고리의 다른 글
| Boolean Logic & Logic Gates: Crash Course Computer Science #3 (0) | 2021.10.03 |
|---|---|
| Electronic Computing: Crash Course Computer Science #2 (0) | 2021.10.02 |
| Early Computing: Crash Course Computer Science #1 (0) | 2021.10.01 |
| Crash Course Computer Science Preview (0) | 2021.09.30 |
| Intro to Algorithms: Crash Course Computer Science #13 (0) | 2021.09.28 |