
- 오늘(9/28) 새벽 5시에 일어나 공부한 영상. 5시 기상 인증을 하면서 확보된 새벽 시간에 앞으로 Crash Course의 강좌 40개로 CS의 기초를 닦아 보려고 한다. 총 40개의 영상이고 1일 1 영상씩 소화해 내는 것이 목표이다.
- 캐리안 쌤의 빠르지만 정확한 딕션으로 단 10분 만에 알고리즘에 대한 맛보기를 할 수 있는 강의이다. 한국어 자막도 있어서 유용하다.
- 요즘 알고리즘을 풀고 있어서 13번째 영상 주제인 알고리즘으로 정했다. 40개를 순서대로 보면 약간 지루함도 있을 것 같아서, 끌리거나 나에게 필요한 것으로 선택하여 보되, 큰 흐름은 놓치지 않도록 해야겠다. (영상 초반에 각 영상들은 의존 관계에 있지 않다고 하긴 했었다.)
- 다양한 알고리즘 중 Selection Sort(선택 정렬), Merge Sort(합병 정렬), Graph Search(그래프 검색)을 대표적으로 소개하고 있다. 다른 알고리즘에 대해서는 스스로 더 찾아보며 공부할 것.
같은 결과를 도출해 낼지라도 어떤 알고리즘이 다른 알고리즘보다 더 우수할 수 있다. 일반적으로 계산에 소요되는 단계가 줄어들수록 더 좋지만, 사용하는 메모리 양과 같은 다른 요인들도 고려해야 한다. 효율적인 알고리즘을 만드는 것은 현대 컴퓨터 이전에도 존재했던 문제이다.
컴퓨터 과학에서 정렬은 가장 중요한 알고리즘 중 하나이다. 컴퓨터는 항상 정렬한다. 정렬에 관한 알고리즘만 해도 수십 가지가 된다. 이번 영상에서는 정렬 두 가지를 알아본다.
Selection Sort
1. 값을 하나씩 스캔하면서 가장 작은 값을 찾는다.
2. 값을 오름차순으로 정렬하기 위해 가장 낮은 값을 맨 앞에 있는 값과 바꾼다. 이렇게 하면 하나가 정렬된 것이다.
3. 이제 동일한 절차를 반복하는데, 이미 정렬한 숫자 다음부터 시작한다.
Pseudo Code
function selectionSort(array)
// 배열 안의 각 위치를 맨 위부터 맨 아래까지 순환한다.
for i = 0 To end of array
// 각 위치에 대해 배열에서 위치를 바꿀 가장 작은 수를 찾을 때까지 반복 실행
smallest = i
for index = i + 1 To end of array
If array item index < array item smallest
smallest = index
End If
Next
swap array items at index and smallest
Next
Return array- 위의 코드는 for loop가 중첩되어 있다. 이 말은 n개의 항목을 정렬하고 싶다면 n번 반복해야 한다는 뜻이다. 반복 횟수는 n X n이므로 n의 제곱이 된다. 이것이 곧 복잡도이다. 이것은 Big O notation으로 표기하는데, 알고리즘의 속도에 대한 근사치를 제공해 준다.
- 선택 정렬은 정렬하려는 숫자가 증가하면, 필요한 시간도 매우 빠르게 증가한다. 매우 큰 수를 정렬할 때는 적합하지 않은 알고리즘이라고 할 수 있다.
Merge Sort
1. 가장 먼저 배열의 크기가 1보다 큰지 확인한다.
2. 1보다 큰 경우, 배열을 2개로 쪼갠다.
3. 원소가 각 배열에 1개만 남아 있을 때까지 배열을 계속해서 쪼갠다.
4. 각 배열의 첫 숫자를 비교해서 더 낮은 수를 첫 번째 수로 가져오고, 다른 수를 마저 합친다.
- 합병 정렬의 복잡도는 O(n*logn)이다. n은 비교하고 합병하는 데 필요한 횟수만큼 발생하는데, 이 횟수는 정렬 안의 배열 항목 수와 직접 비례한다.
- logn은 병합 단계의 수에서 나온다. 8개의 항목인 배열을 4,2,1개로 쪼갰다. 즉 3번을 쪼갠 것이다. 이런 식으로 반으로 나누는 것은 항목 수 사이에 로그 관계(logarithmic relationship)를 가지고 있다. 2를 밑수로 하는 log 8은 3과 같다.
- 배열의 크기가 2배가 되어 16이라면 2를 밑수로 하는 log16은 4이므로, 분할 단계 횟수는 1이 증가한다. 배열의 크기를 8에서 1,000배인 8000으로 늘려도 분할 단계 수는 꽤 낮다. 2를 밑수로 하는 log 8000은 대략 13 정도 된다. 이래서 병합 정렬이 선택 정렬보다 훨씬 효율적이다.
Graph Search
- 여기서 말하는 Graph란, 선으로 연결된 Node Network를 말한다.
- 이것을 도시들, 그리고 도시들을 연결하는 도로로 된 지도라고 생각해 보자. 도시들 간의 경로는 이동 시 각각 다른 시간이 걸린다.
- Highgarden에서 Winterfell로 갈 수 있는 가장 빠른 경로를 찾을 때 어떤 방법이 있을까?
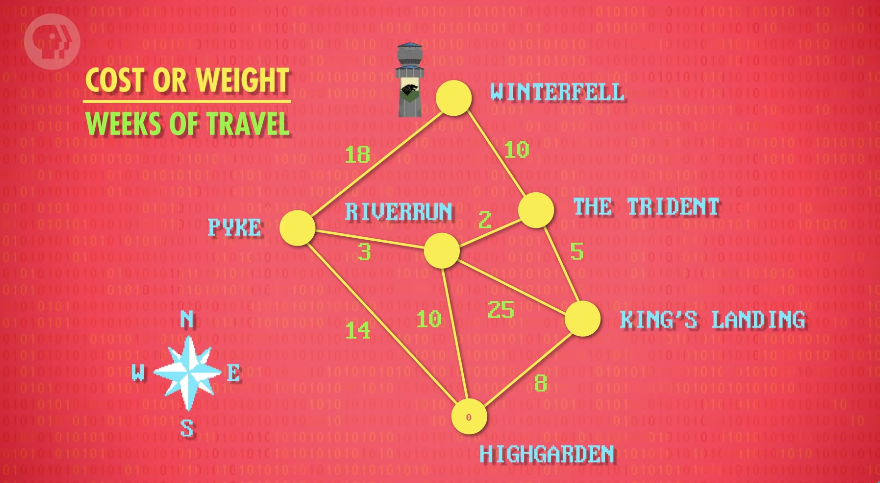
- Brute force approach : 무차별적 접근
- 무차별적 접근은 가장 간단한 방법으로, 모든 단일 경로를 다 조사하여 각각의 총 비용을 계산하는 것이다. 이것을 순열에 적용한다면 모든 순열을 조사하여 정렬 여부를 확인하는 것이다.
- 이것은 n factorial의 복잡성을 가진다. O(n!) 노드의 수인 n부터 시작해 n-1, n-2... 1까지 곱한 것이다. n^2보다 더 오래 걸린다.
- Dijkstra Algorithm Origianl Version : O(n^2)
- 무차별적 접근보다 나은 알고리즘이다. 1956년에 구상되었으며, 그래프 안의 노드 수의 제곱만큼의 복잡도를 가진다. 하지만 이것 역시 좋은 알고리즘이라고 할 순 없다. 미국 전체의 도로 지도와 같이 넓은 범위의 알고리즘 문제는 해결할 수 없기 때문이다.
- Dijkstra Algorithm Better Version : O(n * log n + 1)
- 몇 년 뒤 이 알고리즘은 개선되었다. 그래프 안의 노드 수를 로그와 곱하고, 라인의 수를 더하는 방법이다. 식은 복잡해 보이지만, 꽤 빠르다.
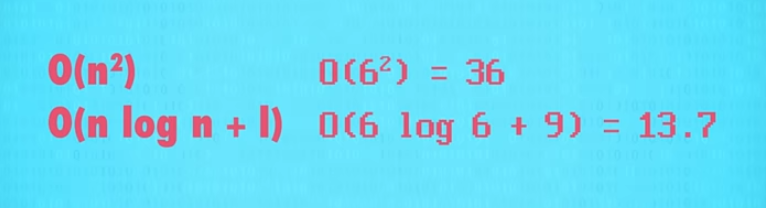
Google map에서 길을 찾는 등의 서비스를 쓸 때마다 Dijkstra Algorithm은 서버에서 실행되어 최적의 길을 찾는다.
정렬과 마찬가지로, 수많은 장단점을 가진 그래프 검색 알고리즘이 무수히 많다. 알고리즘은 어디에나 있으며, 현대는 알고리즘 없이 불가능하게 되었다. 지금까지는 알고리즘의 빙산의 일각만을 다루었지만, Computer Scientist가 되는 핵심은 기존 알고리즘을 사용해서 필요에 따라 새로운 알고리즘을 작성하는 데 있다.
Algorithms are everywhere and the modern world would not be possible without them.
We touched only the very tip of the algorithm iceberg in this episode, but a central part of being a computer scientist is leveraging existing algorithms and writing new ones when needed.
마지막 문장이 인상이 깊어서 옮겨 왔다. Computer Scientist가 된다는 것은 알고리즘과 깊은 연관이 있다는 것. 나도 이 영상을 계기로 알고리즘 세계로 입문하여 실제 세상의 문제를 해결해 나가고 싶다.
'Computer Science > Crash Course' 카테고리의 다른 글
| Boolean Logic & Logic Gates: Crash Course Computer Science #3 (0) | 2021.10.03 |
|---|---|
| Electronic Computing: Crash Course Computer Science #2 (0) | 2021.10.02 |
| Early Computing: Crash Course Computer Science #1 (0) | 2021.10.01 |
| Crash Course Computer Science Preview (0) | 2021.09.30 |
| Data Structures: Crash Course Computer Science #14 (0) | 2021.09.29 |