
Last episode
- How numbers can be represented in binary
Today's episode
- Representing and storing numbers is an important function of a computer, but the real goal is computation or manipulating numbers in a structured and purposeful way, like adding two numbers together.
- These operations are handled by a computer's Arithmetic and Logic Unit, but most people call it by its street name : the ALU.
The mathmatical brain of a computer, ALU
- ALU란, "컴퓨터의 수학적인 뇌"라고도 할 수 있는 산술 논리 장치
- When you understand an ALU's design and function, you'll understand a fundamental part of modern computers.
- ALU is THE thing that does all of the computation in a computer. So basically everything uses it.
The most famouse ALU ever, the Intel 74181

- When it was released in 1970, it was the first complete ALU that fit entirely inside of a single chip - which was a huge engineering feat at the time.
- 오늘 배울 8bit ALU와는 달리 이것은 4bit의 입력만 처리할 수 있었다.
- The 74171 used about 70 logic gates, and it couldn't multiply or divide.
- But it was a huge step forward in miniaturization, opening the doors to more capable and less expensive computers.
We're going to take those Boolean logic gates to build a simple ALU circuit with much of the same functionality as the 74181.
An ALU is two units in one - an arithmetic unit & a logic unit
ALU는 하나에 두 개의 구성 단위가 있는 것. - 산술 단위 & 논리 단위. 이것들을 하나씩 알아보자.
1. Arithmetic unit
- It is responsible for handling all numerical operation in a computer like addition and subtraction.
- It also does a bunch of other simple things like add one to a number, which is called an increment operation.
Adding two numbers together
- We could build this circuit entirely out of individual transistors, but that would get confusing really fast.
- So instead, we can use a high-level of abstraction and build our components out of logic gates, in this case : AND, OR, NOT and XOR gates.
- The simplest adding circuit that we can build takes two binary digits, and adds them together.
- Two inputs(A & B) and one output(the sum of those two digits) - A, B and the output are all single bits.
There are only four possible input combinations.

- In binary, 1 is the same as true, and 0 is the same as false.
- So this set of inputs exactly matches the boolean logic of an XOR gate, and we can use it as out 1-bit adder.

- 1 + 1을 할 때 생기는 carry bit을 위해 컬럼을 하나 더 만들었다.
- The carry bit is only "true" when the inputs are 1 AND 1, because that's the only time when the result (two) is bigger than 1 bit can store.
- 그래서 XOR gate와 AND gate를 합한다. ⇒ Half Adder의 탄생!
Half Adder



- two inputs - bits A and B
- two outputs - the sum and the carry bits
What if you want to compute more than 1+1?
If you want to add more than 1 + 1, we're going to need a "Full Adder". That half-adder left us with a carry bit as output.

이 말은 다중 열 추가 계산에서 다음 열로 넘어갈 때, 모든 열 이후에 2비트가 아닌 3비트를 더해야 한다는 말. 파란 색 부분으로 된 숫자는 총 3개이다.
Full Adder
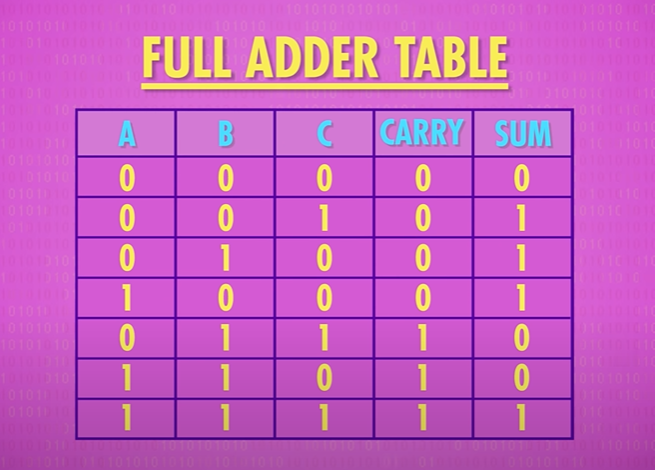
- 입력을 3bit까지 가능(A,B,C)하다. 그래서 가능한 최대 입력은 표의 가장 밑에서도 알 수 있듯 1+1+1이 된다.
- 1을 올려받고 여전히 두 개의 출력선(output wires)이 필요하다. (sum and carry)
We can build a full adder using half adders.
- To do this, we use a half adder to add A plus B - just like before - but then feed that result and input C into a seconde half adder. (A,b 더할 땐 반가산기 쓰고, 그 결과를 C와 함께 두 번째 반가산기에 입력한다.)
- 마지막으로 캐리비트 중 하나가 참인지 확인하기 위해 OR gate가 필요하다.

3개의 입력을 받아 그것들을 더하고, 출력으로 만약 1이 있다면 sum과 carry bit을 더하면 된다.
8-bit ripple carry adder

- A0 + B0 부터 더해 보자. 여기서 처리할 Carry bit는 없기 때문에 Half Adder를 쓴다. 첫 번째 덧셈이기 때문이다.
- 출력은 sum0이라고 하고, 다음으로 넘어가면 A1과 B1을 더하는 것이다.
- 이전의 A0과 B0의 합에서 Carry bit가 나올 가능성이 있기 때문에 이번에는 Full Adder를 사용하고, Carry bit을 입력한다. 이 결과를 sum1으로 출력한다.
- 이런 식으로 8bit가 모두 추가될 때까지 작업이 사슬 안에서 계속된다.
- Carry bit가 다음 Full Adder로 전달이 된다 - 그래서 "8-bit ripple carry adder"라고 한다. ripple은 잔물결, 혹은 파문처럼 퍼진다는 뜻이다.
그런데 마지막의 Full Adder를 주목하자. 만약 9번째 비트가 carry에 있게 되면, 두 숫자의 합이 8bit에 들어가기엔 너무 크다는 의미이다. 이것을 바로 Overflow라고 한다.
overflow
- In general, an overflow occurs when the result of an addition is too large to be represented by the number of bits you are using.
- This can usually cause errors and unexpected behavior.
How to avoid overflows
- We can extend out circuit with more full adders, allowing us to add 16 or 32 bit numbers.
- This makes overflows less likely to happen, but at the expense of more gates.
- An additional downside is that it takes a little bit of time for each of the carries to ripple forward.
위와 같은 이유로 현대 컴퓨터는 "Carry-Look-Ahead Adder"라는 약간 다른 덧셈 회로를 이용한다. 이진수를 더하는 일을 더 빠르게 할 수 있다.
ALU에 곱셈과 나눗셈 연산은 없다. 단순한 ALU는 이를 위한 회로를 가지고 있지 않기 때문이다. 대신에 곱셈을 하려면 여러 번 덧셈을 하는 식으로 추가 작업을 한다. 많은 다양한 단순한 프로세서들은 이런 식으로 작동한다. Thermostat, TV remote, microwave에 있는 프로세서들은 이런 식으로 곱셈한다. 대신 속도가 좀 느리다.
하지만 스마트폰, 노트북 등에 있는 고급 프로세서들은 곱셈 전용 회로가 있는 arithmetic unit을 가지고 있다. 이 회로는 덧셈 회로보다는 복잡하다. 더 많은 논리 게이트(logic gate)가 필요하기 때문이다. 가격이 낮은 프로세서는 이 기능을 갖고 있지 않다.
2. Logic unit
The other half of the ALU - Logic unit
- 이것은 산술 연산 대신, AND, OR, NOT과 같은 논리 연산을 한다.
- 어떤 숫자가 음수인지 확인하는 것과 같은 간단한 숫자 테스트를 하기도 한다.
8-bit ALU

8-bit ALU는 완전히 구축하려면 수백 개의 logic gate가 필요하다. 굉장히 복잡한데, 이것을 추상화해서 큰 V자 모양으로 그려내었다.
8-bit ALU has two inputs, A and B, each with 8 bits.
ALU는 덧셈과 뺄셈을 할 때 4bit 연산 코드를 사용한다. 연산 코드가 ALU에게 무슨 연산을 해야할지를 알려준다.
- 1000 : 덧셈 명령
- 1100 : 뺄셈 명령
A와 B를 입력한 연산의 결과는 8bit로 출력된다.
Flags
ALU는 특정 상태, 상황에 대해서 1bit로 일련의 신호를 출력하기도 한다. 이것을 flag라고 한다.
1. zero flag
두 수를 뺄셈했을 때 결과가 0이라면, 이미 만들어져 있는 0 테스트 회로가 0 flag를 1로 놓는다. 이것은 두 수가 같은지 판단할 때 유용하다.
2. Negative flag
A < B인지 테스트하고 싶다면 ALU를 사용해서 A-B를 하고, 음의 신호가 참인지 보면 된다.
3. Overflow flag
Full Adder를 수행하기 위해 부여된 선도 있다. Overflow가 있다면 이것을 Overflow sign이라고 부를 것이다.
Fancier ALUs will have more flags, but these three flags are universal and frequently used.
We'll be using them soon in a future episode.
여기까지 컴퓨터가 기본적인 수학 연산을 기어, 레버 없이 디지털적으로 수행하는 방법을 배웠다.
이러한 ALU를 CPU를 구성하기 위해 이후 두 에피소드에서 사용할 것이다.
그 전에 컴퓨터에는 메모리가 필요한데, 이건 바로 다음 에피소드에서 배운다.
ALU라는 것이 굉장히 생소했지만, 컴퓨터가 연산을 할 때 어떤 식으로 작동하는지 큰 틀을 파악하는 데 좋은 영상이었다. 역시 한 번 봐서는 완전히 알 수 없는 것 같고, 여러 번 보고 다른 자료도 찾아봐야 컴퓨터와 좀 더 가까워질 것이다.
이 코스 전반적으로 추상화가 정말 자주 나오는데, 덕분에 추상화의 중요성을 실감할 수 있었다. 복잡한 것이 가려지니까 더 복잡한 것에 도전할 수 있게 되었다는 말이 와닿는다.
'Computer Science > Crash Course' 카테고리의 다른 글
| The Central Processing Unit (CPU): Crash Course Computer Science #7 (0) | 2021.10.08 |
|---|---|
| Registers and RAM: Crash Course Computer Science #6 (0) | 2021.10.06 |
| Representing Numbers and Letters with Binary: Crash Course Computer Science #4 (0) | 2021.10.04 |
| Boolean Logic & Logic Gates: Crash Course Computer Science #3 (0) | 2021.10.03 |
| Electronic Computing: Crash Course Computer Science #2 (0) | 2021.10.02 |